Application.Union

Application.Union　　　2011.01.30

Application.Unionメソッドは、2つ以上のセル範囲の集合を返します。Rangeオブジェクトを多く使用する場合に重宝します。その機能と特徴を知ることで、プログラムの幅が広がると思います。

機能、構文と使用例

機能：2つ以上のセル範囲の集合を返す
構文：式.Union(Arg1, Arg2, ...)

式は省略可能です。Application オブジェクトを返すオブジェクト式を指定します。
引数のArg1,Arg2,...は、Rangeオブジェクトを表し、集合させるセル範囲を指定します。
引数は30まで指定可能です。そのうち第1引数と第2引数は必須です。

名前を定義したセル範囲やSpecialCellsメソッドで取得のセル、そして、Rows・ColumnsプロパティもRangeオブジェクトを返すので、指定が可能です。

Sub Ex_Union_1() '使用例
    Dim objUnion As Range
    Range("A1:B3").Name = "AreaA"
    Range("D1,E2,F5").Value = 1
    Set objUnion = Union( _
                    Range("AreaA"), _
                    Range("D1:F5").SpecialCells(xlCellTypeConstants, 1), _
                    Rows(6), _
                    Columns(7))
    MsgBox objUnion.Address(False, False) '結果[A1:B3,D1,E2,F5,6:6,G:G]
End Sub

Unionメソッドの応用（1）

セル範囲を動的に集合

Unionメソッドを用い、セル範囲を動的に集合させる例です。

Sub Ex_Union_2()
    Dim i As Integer
    Dim objUnion As Range
    Set objUnion = Cells(1, 1)
    For i = 3 To 11 Step 2
        Set objUnion = Union(objUnion, Cells(i, 1))
    Next
    MsgBox objUnion.Address(False, False) '結果[A1,A3,A5,A7,A9,A11]
End Sub

Unionメソッドの応用（2）

セルアドレスの最適化

Unionメソッドはセル範囲を集合させる際に、セルアドレスを最適化する特徴をもっています。隣り合ったセルや隣り合った列を、別の引数に指定した場合は、アドレスを最も合理的なかたちに変換します。

Sub Ex_Union_3()
    Dim objUnion As Range
    Set objUnion = Union(Range("A1:A3"), Range("B1:F3"))
    MsgBox objUnion.Address(False, False) '結果[A1:F3]
End Sub

セルアドレス最適化の応用

セルアドレス最適化の特徴を用いた応用です。
下の例は、第1引数、第2引数に同じRangeオブジェクトを指定しています。
Rangeオブジェクトには、連続したそれぞれの行を指定し、Unionメソッドで、1つの行範囲（セル範囲）に最適化しています。

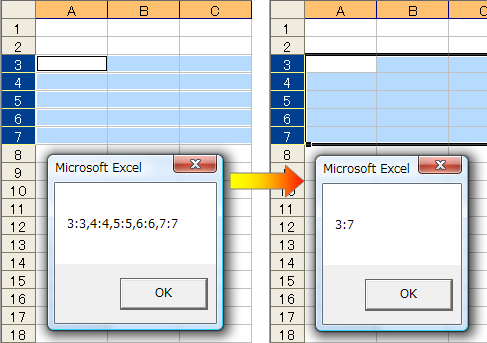
Sub Ex_Union_4()
    Dim objUnion As Range
    Set objUnion = Range("3:3,4:4,5:5,6:6,7:7")
    objUnion.Select
    MsgBox objUnion.Address(False, False) '結果[3:3,4:4,5:5,6:6,7:7]
    '同じRangeオブジェクトを第1,第2引数に指定
    Set objUnion = Union(objUnion, objUnion)
    objUnion.Select
    MsgBox objUnion.Address(False, False) '結果[3:7]
End Sub

Unionメソッド使用の留意点

処理時間

Unionメソッドは、セルを集合させる、アドレスを最適化するといった重宝する機能をもっていますが、場合によっては処理に時間のかかることがあります。引数の数が多くなったり、アドレスが長い場合は注意が必要です。用途に応じ、使い分けることが大切です。

VBA Tips

VBA高速化検証1

VBA高速化検証2

セルの塗りつぶし